Polymers at Interfaces
Adsorption Isotherm for Polymers
The adsorption of polymers from dilute polymer solutions was investigated in great detail in the 1960s and 1970s.1-7 Most of these models describe either the behavior of isolated polymers near interfaces or the adsorption of polymers from homogenous polymer solutions.
One of the oldest and simplest models was developed by Hoeve et al. in the mid 1960s and early 1970s.1,5,6 Hoeve, DiMarzio and coworkers assumed that a system of a very dilute polymer solution in contact with a weakly absorbing barrier can be divided into two distinct regions: the interface layer having a surface area A , and the very dilute polymer solution of volume Vs. Since the polymers are attracted by the interface, polymer segments will accumulate at the interface. This layer has the thickness δ corresponding to the effective thickness of the segments. Beyond this layer, the segments will not be directly attracted by the interface, although indirectly since they are part of tails and loops that come frequently in contact with the interface. If the polymers are only weakly adsorbed onto the substrate, that is if only a small fraction of the monomers is in contact with the adsorbing interface, the polymers will frequently desorb and escape the interface region. Thus the adsorbed polymers will be in a thermodynamic equilibrium with the polymers in the solvent phase.
As has been shown by Hoeve, the free energy of such a polymer-solvent system can be divided into the free energy of the individual polymer coils and the entropy resulting from the macroscopic partition of the polymer coils over the whole system. However, this is only possible if the polymer coils in solution do not overlap. Otherwise a mean-field approach is more appropiate as suggested by Roe and others,3,7 since there are no distinctive microscopic and macroscopic "phases".
Polymers near an Adsorbing Interface
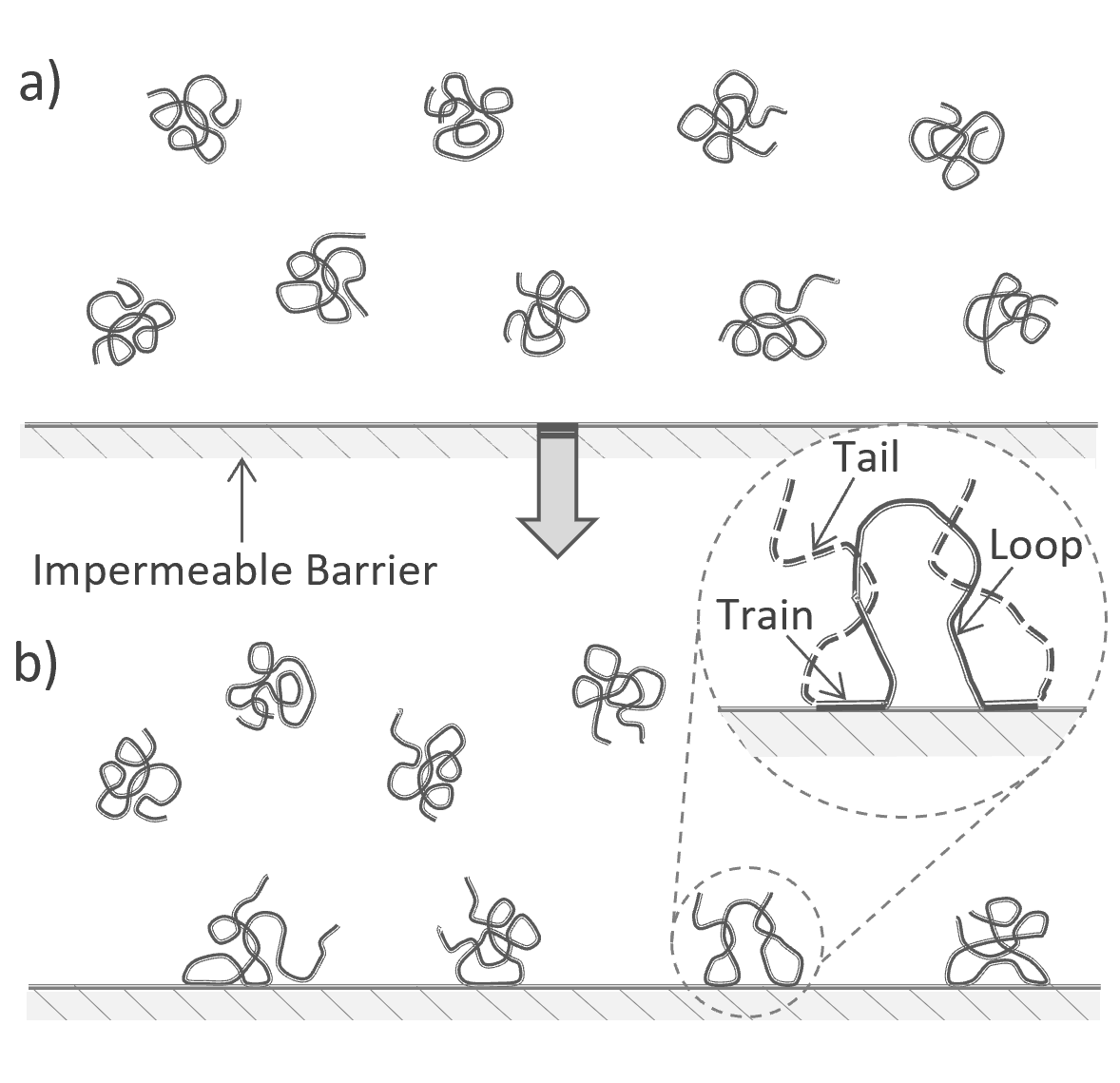
Polymers near an Adsorbing Interface
Hoeve, DiMarzio and Peyser1 assumed that the solvent and polymer molecules are randomly distributed over the solvent volume and the interface. A polymer is regarded as adsorbed when at least one repeat unit is within a distance δ from the surface. The adsorption isotherm of such a system can be derived from the partition function Q of the whole system. Choosing a simple lattice model, the lattice can be divided into M identical layers with L identical lattice sites.3 Each solvent molecule and each of the r identical repeat units of the polymer molecules occupy exactly one lattice site of volume v. Then the total number of lattice sites ML equals the total number of segments and solvent molecules,
ML = rNp + Ns
where Np is the total number of polymer chains and Ns is the number of solvent molecules. Np,a of the Np polymer molecules will be in contact with the interface and Np,s remain in solution. The total number of ways to distribute Np,a adsorbed molecules over L surface lattice sites reads8
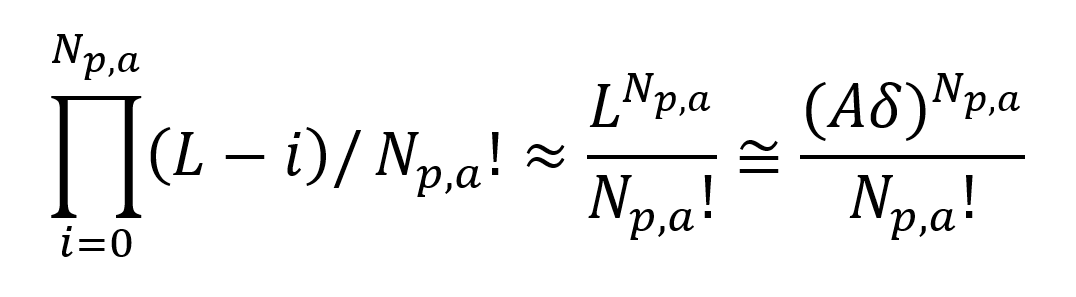
The Np,s molecules not in contact with the interface can be placed on any of the L(M -1) remaining lattice sites. The expression for the total number of placements of these chains reads
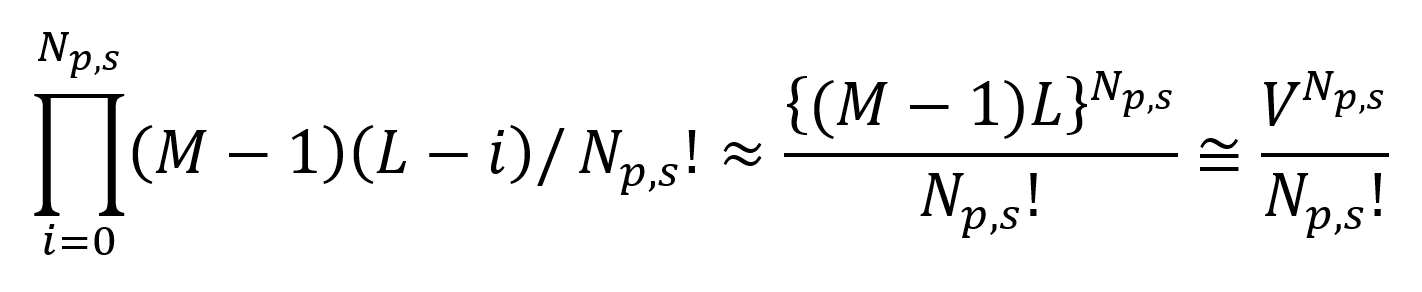
Thus for the lattice model the partition function can be written as
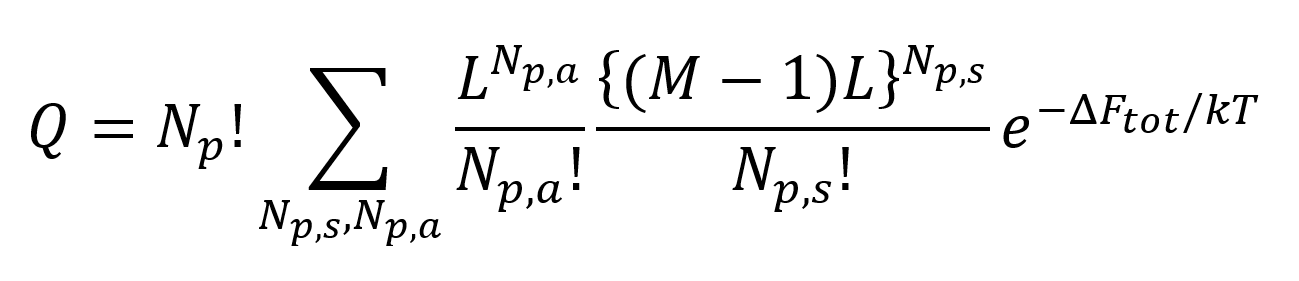
where ΔFtot is the change of Helmholz energy of mixing when Np,a polymer coils are adsorbed at the interface. Np!/(Np,a! Np,s!) is the number of ways of distributing the molecules over the adsorbed state and that in solution. The summation is over all possible values of Np,a and Np,s. The most probable distribution (the maximum) can be calculated with the method of Langrangian multipliers with the restriction Np,a + Np,s = Np. We obtain then following equation for the adsorption isotherm:
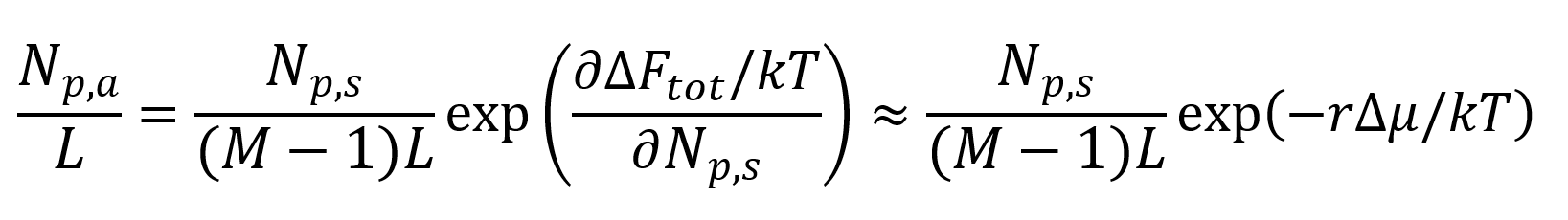
and with δA = vL and (M -1)Lv = V:1,5
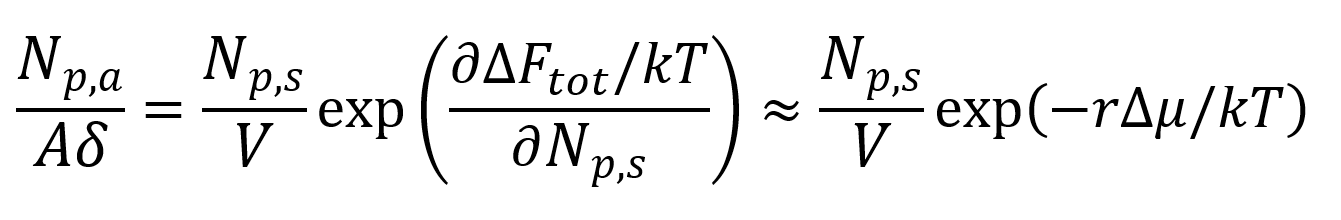
Where Δμ is the average Helmholz free energy per segment. This quantity can be predicted using classical thermodynamics and Flory-Huggins theory of mixing.5-7.
The Hoeve-DiMarzio-Peyser approach is only recommended for very dilute polymer solutions (no overlap of polymer coils in solution) and to interfaces with low surface coverage which greatly limits its usefullness in terms of making quantitative predictions. In the case of high surface coverage a mean-field approch as suggested by Roe, Scheutjens and Fleer3,7 yields more accurate results.
References and Notes
C. A. J. Hoeve, E. A. DiMarzio u. P. Peyser, J. Chem. Phys. 42, 25 (1965)
E.A. DiMarzio, F.L. McCrackin, J. Chem. Phys. 43, 539 (1965) & 43, 2392 (1965)
R. J. Roe, J. Chem. Phys. 60, 4192 (1974)
A. Silberberg, J. Chem. Phys. 46, 1105 (1967) und 48, 2835 (1968)
C. A. J. Hoeve, J. Chem. Phys. 44, 1505 (1965)
C. A. J. Hoeve, J. Polymer Sci. C 30, 361 (1970) & C 34, 1 (1971)
J.M. Scheutjens, G.J. Fleer, J. Phys. Chem. 83, 1620 (1979) & 84, 178 (1980)
Note that this expression does not include the number of internal conformations of each polymer molecule. Thus, the total number of possible placements of Ns solvent molecules and Np r segments over ML latice sites is the product of all possible translational arrangements, (e.g. possible placements of the fiirst (adsorbed) segment over the ML lattice sites) and the number of internal conformations of all polymer molecules. Only when r = 1 are both expressions identical.
January 21, 2019; Revised June 8, 2019